Convolutional Neural Networks

In its most basic form, a neural network is a set of multilayered, interconnected nodes, often referred to as neurons. Each neuron receives input from neurons in the previous layer, performs a computation, and passes the result to the neurons in the next layer. The simplest neural network, a single-layer perceptron, consists of a set of input nodes, each connected to the output node. To address more complex tasks and learn non-linear relationships, multi-layer neural networks can be used. These networks consist of multiple layers of neurons, including one or more hidden layers between the input and output layers. These networks are often referred to as deep neural networks, given their multiple hidden layers.

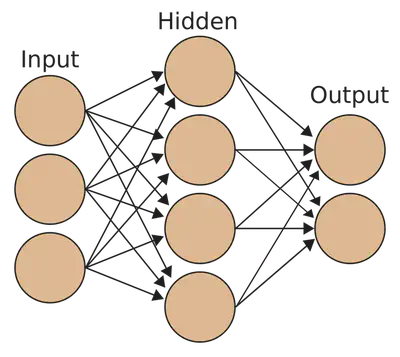
As was previously mentioned, when a neuron receives input from the previous layer, it performs a mathematical computation on its inputs. The simplest computation performed is the weighted sum of inputs, yielding a linear transformation of the input data. Oftentimes, more complex functions, known as activation functions, are applied to the weighted sum of the inputs. These functions allow the network to learn more complex relationships, such as non-linear relationships. One of the most popular activation functions is the rectified linear unit or ReLU, which returns the input as the output if it is positive, and zero otherwise.

Convolutional Neural Networks

A convolutional neural network (CNN) is a specialized type of DNN that is designed for processing and analyzing structured grid-like data such as images or time series. Rather than analyzing the entire input dataset at once, a CNN can be thought of as analyzing specific regions of the data. These networks utilize convolutional layers, which apply filters or kernels to the data to extract isolated features. Having extracted features from the data, another common step is to subsample or pool the data to reduce the computational complexity of the data, making the network more robust.

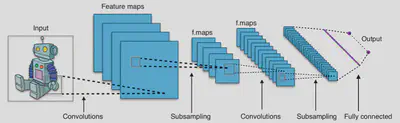
Challenges of Multilayered Networks

For complex networks with many layers, after applying a convolutional layer, the distribution of the input data can drastically change, leading to challenges in training. Batch normalization is a technique employed to combat these difficulties, improving training stability and accelerating convergence by normalizing the inputs to each layer.

Another challenge with multilayered CNNs stems from the way in which model parameters are adjusted. In traditional networks, information flows sequentially through each layer. Parameters are updated by flowing backward through these layers in a process known as backpropagation. During the backpropagation algorithm, gradients are computed with respect to the network’s parameters by propagating the error signal from the output layer to the input layer. These gradients are then used to update the weights of the network in order to minimize the loss function. However, in deep networks, the gradients can diminish exponentially as they pass through multiple layers, making it difficult for the network to learn effectively. One approach to counteract this problem is using skip connections that alter the flow of information by bypassing layers.

Avoiding Overfitting

Given the inherent complexity in CNNs, it is understandable that models may overfit and not be generalizable to testing data. To avoid this, a number of strategies can be employed, such as reducing the model complexity, either by reducing the number of parameters or the number of hidden layers. Alternatively, we can make the data noisy or harder to learn. One such example is the use of dropout, where a random set of neurons is temporarily deactivated during training. In other words, the model is no longer allowed to use those neurons as a source of information. By limiting the number of neurons the model may use, dropout forces the network to use more robust and generalizable features. Importantly, as the model is trained, the deactivated neurons will change randomly. During testing, dropout is usually turned off, and the full network is used without any dropped-out neurons. However, the weights of the network are typically scaled down by the dropout probability to account for the increased number of active neurons during testing.